Bagaimana hasil SBMPTN kamu? Bagi semua yang belum lolos di ujian tersebut, jangan bersedih. Masih ada kesempatan lain yang bisa kamu tempuh untuk masuk universitas impianmu. Jika kamu ingin masuk ke UGM, kamu masih bisa mengikuti seleksi mandiri yang diadakan pihak kampus. Sebelum itu, kamu juga perlu mempersiapkannya dong. Yuk, latihan soal UTUL UGM kemampuan dasar matematika berikut.
Latihan Soal Kemampuan Dasar Matematika UTUL UGM
1. Parabola y=-x2+ 2ax+a-2 dan garis y= ax+a-2 berpotongan di (x1,y1) dan (x2,y2). Jika x1+x2=2, maka y1+y2=…
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan:
Diketahui Parabola y=-x2+ 2ax+a-2 dan garis y= ax+a-2 berpotongan, maka
Subtitusi a=2 ke persamaan garis
untuk a=2 dan x1= 0
Oleh karena itu, diperoleh titik potong (x1,y1) = (0,0)
Untuk a=2, x1=a=2
Oleh karena itu, diperoleh titik potong (x1,y1) = (2,4)
Sehingga berakibat Y1+Y2 = 4
Jawaban: E
2. Jika (b+c, b, c) memenuhi sistem persamaan 
maka b+c +…
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan:
Diperhatikan bahwa solusi dari sistem persamaan linier 
Adalah 
sehingga berakibat x = b+ C, y = b, dan z = c. Oleh karena itu, apabila
disubtitusikan ke sistem persamaan linier diatas, didapatkan:
Eliminasi persamaan (i) dan (ii), didapat 
subttusi nilai c = -1 ke persamaan (ii), didapat 
jadi, didapat b + c = 1
Jawaban: B
3. Nilai 1 – x yang memenuhi persamaan 
adalah…
A. -4
B. -3
C. -2
D. 3
E. 4
Pembahasan:
Diketahui 
perhatikan 
Oleh karena itu, diperoleh 1- x= 1- (-3) = 4
Jawaban: E
4. Jika 
dan I matriks identitas, maka AB-1+ BA-1 =…
A. 1/3 I
B. 1/2 I
C. I
D. 2I
E. 3I
Pembahasan:
Diketahui, 
Perhatikan, 
oleh karena itu, berakibat 
jadi, AB-1+ BA-1 = 3I
Jawaban: E
5. Jika a+ 2β = 5 dan αβ= -2 maka persamaan kuadrat yang akar-akarnya 
adalah… 
Pembahasan:
Diketahui a+ 2β = 5 dan αβ= -2, missal 
Perhatikan 
dan 
Oleh karena itu, 
Jawaban: E
6. Nilai rata-rata test matematikadi suatu kelas adalah 72. Nilai rata-rata siswa putera adalah &5 dan nilai rata-rata siswa putri adalah 70. Jika banyaknya siswa putri 6 lebih banyak dari siswa putra, maka banyaknya siswa di kelas tersebut adalah….
A. 30
B. 35
C. 40
D. 45
E. 50
Pembahasan:
Diketahui 
Sehingga diperoleh W= L + 6 = 18, Jadi banyaknya siswa di kelas tersebut adalah L + W = 30
Jawaban: A
7. Jika jumlah empat suku pertama dan jumlah tujuh suku pertama di suatu barisan aritmatika berturut-turut 30 dan 84, maka jumlah lima belas suku pertama barisan tersebut adalah…
A. 330
B. 336
C. 345
D. 360
E.
Pembahasan:
Diketahui S4= 30 dan S7, berakibat 
Jadi, jumlah ke lima belas suku pertama barisan aritmatika tersebut adalah 360
Jawaban: D
8. Misalkan ada 2 jalan dari kota A ke kota B, 4 jalan dari kota A ke kota C, 2 jalan dari kota B ke kota C. Dari B dan C masing-masing ada 3 jalan ke kota D. Jika seseorang darikota A pergi ke kota D melalui Kota B atau C atau Kota B dan C, maka banyaknya cara yang dapat ia tempuh adalah…
A. 14
B. 18
C. 36
D. 54
E. 144
Pembahasan:
Perhatikan ilustrasi rute perjalanan berikut.
Rute perjalanan yang di tempuh. 
Jadi, banyaknya cara dari kota A ke kota D melalui kota B atau C atau kota B dan C adalah 6+12+12+24= 54 cara
Jawaban: D
9. suku ke 3, 5, dan 8 suatu deret aritmatika berturut-turut adalah 
2x + 2, 4x – 7. Jika Un meyatakan suku ke- n barisan tersebut, maka suku ke- 2n adalah…
A. 5+ 3n
B. 2 + 6n
C. 2 Un
D. 3 + 2 Un
E. 3n + Un
Pembahasan: 
Diketahui 
Perhatikan, 
Eliminasi persamaan (i) dan (ii) 
Eliminasi persamaan (i) dan (iii) 
Subtitusi persamaan (iv) dan (v) 
Subtitusi nilai x = 9 ke persamaan (iv), diperoleh: 
Perhatikan, 
Jadi, suku ke- 2n dari deret barisan aritmatika tersebut adalah U2n = Un + 3n
Jawaban: E
10. 
Pembahasan:
Diketahui, 
perhatikan 
Selanjutnya, perhatikan 
Oleh karena itu, diperoleh 
Jawaban: D
11. Jika a = 
maka nilai 4 – a adalah ...
A.-20
B.-12
C.-4
D.12
E.20
Diketahui 
perhatikan, 
Oleh karena itu, diperoleh a = -16. Sehingga berakibat 4 – a = 20.
Jawaban: E
12. Persamaan kuadrat 
Mempunyai akar-akar x1 dan x2. Jika 
Jawaban: C
A.-1 atau 3/2
B.¾ atau 1
C.1/16 atau 8
D.1/8 atau 4
E.4 atau 8
Pembahasan:
Diketahui 
mempunyai akar-akar x1 dan x2, maka berakibat 
Perhatikan, 
misal a= 2log m, maka 
oleh karena itu, berakibat 
selanjutnya perhatikan, 
Jawaban: A
13. Sebuah garis menyinggung grafik f(x) = x2 + 3x-1 di titik (2a-1, b), dan menyinggung grafik g (x) = 1/3x3 + 4x + 1, dititik (a, c). Nilai a + b = ….
A.3 atau 41
B.4 atau 20
C.4 atau 42
D.6 atau 29
E.20 atau 42
Pembahasan:
Diketahui sebuah garis menyinggung grafik grafik f(x) = x2 + 3x-1 di titik (2a-1, b), artinya f(2a-1) = b, dan mf= f’(2n-1).perhatikan 
Dan 
Diketahui juga garis tersebut menyinggung grafik g (x) = 1/3x3 + 4x + 1, dititik (a, c), artinya mg = g’ (a). perhatikan 
Karena grafik f dan g mempunyai garis singgung yang sama , maka berakibat 
Substitusi nilai a=1 atau a = 3 ke persamaan (i)
Untuk a = 1 
Sehingga didapat a+b = 4
Untuk a = 3 
Sehingga didapat a + b = 42
Jadi nilai a + b adalah 4 atau 42
Jawaban: C
14. Jika 1- cot α = - 1/3 maka nilai dari sin 2α + cos2α = …
A.17/25
B.1
C.6/5
D.31/25
E.7/5
Pembahasan:
Diketahui 1- cot α= -1/3. Berakibat 
Dengan menggunakan segitiga, diperoleh 
Dengan menggunakan pytagoras, maka 
Sehingga didapat sin a = 3/5 dan cos a = 4/5. Perhatikan, 
Jadi, nilai sin 2a + cos 2a = 31/25
Jawaban: D
15. Hasil penjumlahan semua penyelesaian 
Oleh karena itu, diperoleh HP= 
sehingga diperoleh 
Jawaban: E
untuk 0 ≤ x < 2µ adalah …
A.4/3 µ
B.2 µ
C.8/3 µ
D.10/3 µ
E.14/3 µ
Pembahasan:
Perhatikan 
Diperoleh 
16. Jika x dan y memenuhi sistem persamaan 
Misal 
didapat 
Eliminasi persamaan (iii) dan (iv) 
Subtitusi n = -4 ke persamaan (iii), di dapat 
Subtitusi kembali nlai m dan n ke permisaan di atas, diperoleh 
Oleh karena itu, diperoleh 
Jawaban: C
maka x + y = …
A. -2
B. -1
C. – 11/ 12
D. – 5/6
E. – 3/4
Pembahasan:
Diketahui, sistem pertidaksamaan 
17. Semua nilai x yang memenuhi 
Jika diberikan fungsi √f(x) maka syaratnya adalah f(x)≥ 0. perhatikan 
dengan mengiriskan kedua garis bilangan, diperoleh
adalah…
A. x ≤ 7/4
B. 1 ≤ x ≤ 7/4
C. x ≤ 1 atau 7/4 ≤ x ≤ 2
D. x ≤- 7/4 dan 1 < x ≤ 2
E. x < 1
Pembahasan:
Perhatikan, 
Pembilang 
Untuk solusi x = -2 tidak memenuhi karena apabila didistribusikan ke 3 √2-x – 2(x-1) hasilnya tidak sama dengan nol, yaitu 
Penyebut, 
Dengan menggunakan garis bilangan, diperoleh 
18. Jika m > 0, maka himpunan semua penyelesaian pertidaksamaan 
adalah…. 
Pembahasan:
Diketahui 
dengan m > 0
Maka 1. Nilai akar mempunyai solusi 
Dengan menggunakan garis bilangan, diperoleh 
Oleh karena itu, m yang memenuhi adalah –m ≤ x ≤ m atau HP1 = 
Langkah 2. 
dengan menggunakan garis bilangan, maka diperoleh 
oleh karena itu, m yang memenuhi adalah 
atau 
atau HP2 = 
dengan membuat irisan dari garis bilangan HP1 dan HP 2, diperoleh garis bilangan 
oleh karena itu, x yang memenuhi menurut garis bilangan diatas adalah 
karena dinyatakan bahwa m> 0, maka dapat disimpulkan bahwa x yang memenuhi adalah 
Jawaban: E
19. Jika 
serta P-1 invers matriks P, maka determinan untuk matriks QP-1 adalah…
A. 3/4 µ
B. 2 µ
C. 8/3 µ
D. 10/3 µ
E. 14/3 µ
Pembahasan:
Diketahui 
diperoleh 
Selanjutnya diperoleh 
Sehingga berakibat 
Jawaban: C
20. Daerah penyelesaian sistem pertidaksamaan linier y ≥ 0, x + y ≤ 2, 3x - 2y ≤ 3, dan -2x + 3y ≤3 adalah… 
Pembahasan:
Dalam hal ini akan digambarkan satu persatu daerah penyelesaian dari pertidaksamaan. Daerah penyelesaian masing-masing, pertidaksamaan adalah daerah yang diarsir.
Untuk x + y ≤ 2 
Untuk 3x – 2y ≤ 3 
Untuk -2x + 3y ≤ 3 
Untuk mempermudah memahami gambar, maka pada gambar dibawah ini, daerah yang diarsir adalah bukan daerah penyelesaian. Hal ini berbeda dari gambar daerah penyelesaiandiatas. Dengan mengiriskanketiga daerah penyelesaian serta daerah penyelesaian untuk x ≥ 0 dan y ≥ 0, diperoleh 
Jadi, grafik himpunan penyelesaian yang tepat adalah pilihan C
Jawaban: C
Ibarat kata orang, masih banyak jalan untuk menuju Roma. Tidak lolos SNMPTN dan SBMPTN bukanlah akhir dari segalanya. Biasanya pihak universitas masih membuka tes jalur mandiri, seperti halnya UGM dengan jalur tes UTUL nya. Kuncinya, kamu harus selalu belajar dan terus berlatih soal. Selain itu, jangan lupakan juga untuk selalu berdoa agar selalu diberikan kemudahan.
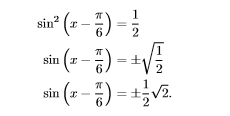
Post a Comment