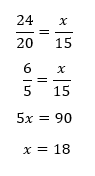Ujian tengah semester semakin dekat, tapi belum menguasai materinya? Nggak perlu khawatir. Karena kamu bisa belajar dengan mengerjakan beberapa soal latihan kelas 7 SMP Matematika ini. Dengan begitu, kamu pun akan bisa mengukur dan mengetahui materi mana saja yang belum kamu kuasai. Tanpa berlama lama, yuk kita mulai berlatih untuk mengerjakan soal berikut ini.
Deretan Soal Latihan Matematika Untuk Kelas 7 SMP
1. Survei yang dilakukan terhadap anak-anak yang di Desa Asri Bumi menampilkan bahwa 20 anak gemar melihat serial Power Ranger, 15 anak gemar dengan serial Barbie serta 19 anak yang tidak suka dengan keduanya. Maka jumlah peserta di dalam survei tersebut ada … anak.
A. 30
B. 31
C. 32
D. 33
Jawaban : B
Pembahasan
S = teorema universal
A = serial Power Ranger
B = serial Barbie
A ∩ B = suka keduanya
dik :
A = 30 anak
B = 20 anak-anak
(A∩ B) = 19 anak-anak
Dit: n (S) …?
Pembahasan: n (S) = (A) + (B) – (A ∩ B)
n (S) = 30 + 20 – 19
n (S) = 31
2. Dari 35 orang anak, terdapat (25 – x) anak yang gemar makan burger dan (18 – x) yang gemar makan kebab. Apabila terdapat 7 anak yang tidak gemar makan burger dan juga kebab, maka jumlah dari anak yang gemar makan keduanya adalah … anak.
A. 3
B. 4
C. 5
D. 6
Jawaban : A
S = teorema universal
P = gemar makan burger
C = gemar makan kebab
T = Tidak suka keduanya
Dik :
S = 35 anak-anak
P = (25 – x)
C = (18 – x)
T = 7 anak-anak
Dit : Anak yang gemar makan kebab …?
Pembahasan : n (S) = n (P) + n (C) + n (P ∩ C) + n (T)
35 = (25 – x) + (18 – x) + x + 7
35 = 50 – x
x = 15
n (C) = (18 – x)
= 18 – 15
= 3
3. Di dalam sebuah kelas terdiri dari 30 siswa. 15 siswa diantaranya gemar bermain basket, 20 siswa lagi gemar bermain volly dan jumlah siswa yang gemar dengan keduanya adalah 8. Lalu, jumlah siswa yang tidak suka dengan keduanya yaitu ….
A. 3
B. 4
C. 5
D. 6
Jawaban : A
Pembahasan
S = teorema universal
A = gemar bermain basket
B = gemar bermain volly
A ∩ B = seperti keduanya
T = tidak suka keduanya
dik :
S = 30 anak
A = 15 anak
B = 20 anak
(A ∩ B) = 8 anak-anak
Dit : Anak yang tidak suka dengan keduanya …?
Jawab: n (S) = ((A) + (B) – (A ∩ B)) + (T)
30 = (15 + 20-8) + n (T)
30 = 27 + n (T)
n (T) = 3
4. Di dalam kelas VII-G terdapat 35 siswa. Setelah diseleksi terdapat 21 siswa menyukai pelajaran olahraga, 20 siswa menyukai Bahasa Indonesia dan 10 siswa suka dengan keduanya. Jumlah dari siswa yang tidak suka dengan keduanya adalah … siswa.
A. 3
B. 4
C. 5
D. 6
Jawaban : B
Pembahasan
S = 35 anak-anak
M (Olahraga) = 21 anak-anak
B (Bahasa Indonesia) = 20 anak
(M ∩ B) = 10 anak-anak
Jumlah anak yang tidak suka dengan keduanya …?
n (S) = (M) + (B) – (M ∩ B) + (T)
35 = (21 + 20-10) + n (T)
35 = 31 + n (T)
4 = n (T)
5. Apabila diketahui A = {10, 11, 12, 13}, B = {jumlah hitungan antara 10 dan 15} sedangkan C = {x | 8 ≤ 5 ≤ 12, x bilangan asli). Maka nilai dari A – (B ∩ C) dan A – (B ∪ C) yaitu ….
A. {11, 12} dan {10, 11, 12, 13}
B. {11, 12} dan {8, 9, 14}
C. {10, 13} dan {10, 11, 12, 13}
D. {10, 13} dan {8, 9, 14}
Jawaban : D
Pembahasan
A = {10, 11, 12, 13}
B = {hitung antara 10 dan 15}
= {11, 12, 13, 14}
C = {x | 8 ≤ x ≤ 12, x є angka alami}
= {8, 9, 10, 11, 12}
A – (B ∩ C) = ({10, 11, 12, 13} – {11, 12})
= {10, 13}
A – (B ∪ C) = ({10, 11, 12, 13} – {8, 9, 10, 11, 12, 13, 14})
= {8, 9, 14}
6. Diketahui bahwa S = {0, 1, 2, …., 20} dan B = {x | x <18, x bilangan asli), maka Bc adalah ….
A. {0,18,19,20}
B. {18,19,20}
C. {0,18}
D. {0}
Jawaban : A
Pembahasan
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 18, 19, 20}
B = {x | x <18, x bilangan asli}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17}
7. Apabila A = {1, 2, 3, 4}, B = {2, 4} serta C = {1, 2, 3, 4, 5}, maka nilai untuk (A ∪ B) ∩ C yaitu ….
A. {1,2,3,4,5}
B. {5}
C. {2,4}
D. {1,2,3,4}
Jawaban : B
Pembahasan
A = {1, 2, 3, 4}
B = {2, 4}
C = {1, 2, 3, 4, 5}
A ∪ B = {1, 2, 3, 4}
(A ∪ B) ∩ C = {5}
8. Jika nilai P = 100, Q = 120 serta nilai dari (P ∩ Q) = 80, maka nilai untuk (P ∪ Q) adalah ….
A. 80
B. 100
C. 120
D. 140
Jawaban : D
Pembahasan
P = 100, Q = 120, dan n (P ∩ Q) = 80
n (A-B) = (P) + (Q) – (P ∩ Q)
= 100 + 120 – 80
= 140
9. Diketahui, jika himpunan A = {jumlah hitung <8} sedangkan B = {faktor 6}. Pada saat Anda mendaftar anggota, maka nilai (A ∪ B) adalah ….
A. 5
B. 6
C. 7
D. 8
Jawaban : D
Pembahasan
A = {angka <8}
= {0, 1, 2, 3, 4, 5, 6, 7}
B = {faktor dari 6}
= {2, 3}
A ∪ B = {0, 1, 2, 3, 4, 5, 6, 7}
n (A ∪ B) = 8
10. Jika diketahui bahwa S = {0, 1, 2, 3, …., 10}, A = {2, 3, 4, 5, 7} serta B = {1, 3, 5, 7, 9}. Maka nilai dari AB adalah …
A. {3, 5, 7}
B. {0, 1, 6, 8, 9, 10}
C. {0, 6, 8, 9, 10}
D. {0, 1, 6, 8, 10}
Jawaban : B
Pembahasan
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {2, 3, 4, 5, 7}
B = {1, 3, 5, 7, 9}
Ac = {0, 1, 6, 8, 9, 10}
11. Diketahui bahwa K = {x | -1 ≤ x ≤ 3; x bulat integer} sedangkan L = {x | 0 <x ≤ 5; x є nomor utama}. Jika K – L, maka hasilnya adalah ….
A. {-1, 0, 1, 2, 3}
B. {-1, 0, 1, 2}
C. {-1, 0, 1}
D. {2, 3, 5}
Jawaban : C
Pembahasan
K = {x | -1 ≤ x ≤ 3; x є integer
= {-1, 0, 1, 2, 3}
L = {x | 0 <x ≤ 5; x є nomor utama}
= {1, 2, 3, 5}
Maka hasil dari K – L = ({-1, 0, 1, 2, 3} – {2, 3, 5})
= {-1, 0, 1}
12. Apabila nilai A = {2, 3, 4} sedangkan nilai B = {1, 3}, maka nilai dari A ∪ B adalah ….
A. {3}
B. {1, 2, 3, 4}
C. {1, 3}
D. {2, 4}
Jawaban : B
Pembahasan
Jika:
A = {2, 3, 4}
B = {1, 3}
Maka nilai A ∪ B = {1, 2, 3, 4}
13. Perhatikan Gambar Berikut
Jika garis m dan n sejajar, maka besar ∠3 di atas adalah ….
A. 20°
B. 40°
C. 60°
D. 80°
Jawaban : D
Pembahasan
Perhatikan bahwa 120° merupakan pelurus dari ∠2.
Sehingga,
∠2 = 180° - 120° = 60°
Kemudian 140° merupakan pelurus dari ∠4
Sehingga,
∠4 = 180° - 140° = 40°
Ingat, bahwa jumlah sudut sudut pembentuk segitiga adalah 180°
Sehingga
∠2 + ∠3 + ∠4 = 180°
60° + ∠3 + 40° = 180°
100° + ∠3 = 180°
∠3 = 180° - 100°
∠3 = 80°
Jadi, untuk besar dari ∠3 adalah 80°
14. Dewi mempunyai uang sebesar Rp8.000,00 dan Amel mempunyai uang Rp2.000,00 lebihnya dari uang Cindy. Perbandingan uang Dewi dan Amel adalah ….
A. 2 : 8
B. 8 : 2
C. 4 : 5
D. 5 : 4
Jawaban : C
Pembahasan
Misalkan uang Dewi = D
uang Amel = A
Maka diperoleh:
D = 8.000
A = D + 2.000 = 8.000 + 2.000 = 10.000
Sehingga,
D : A = 8.000 : 10.000 = 4 : 5
Jadi, perbandingan uang Dewi dan Amel adalah 4 : 5
15. Suatu proyek dapat diselesaikan selama 30 hari oleh 15 orang. Setelah bekerja 6 hari proyek tersebut terhenti selama 4 hari. Jika kemampuan bekerja setiap orang sama, agar pekerjaan selesai tepat waktu, jumlah pekerja tambahan yang dibutuhkan adalah ….
A. 1 orang
B. 3 orang
C. 6 orang
D. 9 orang
Jawaban : B
Perhatikan
30 hari → 15 pekerja
Setelah bekerja 6 hari, maka sisa 24 hari
24 hari → 15 pekerja
Pekerjaan terhenti 4 hari, maka sisa 20 hari
20 hari → x pekerja
Perbandingan di atas merupakan perbandingan berbalik nilai.
Sehingga,
Maka, Pekerja tambahan = 18 – 15 = 3 orang
Jadi, jumlah pekerja tambahan yang dibutuhkan adalah 3 orang.
16. Pada bentuk aljabar x² – 2x – 5 koefisien-koefisiennya adalah ....
A. x²
B. -2
C. - 2x dan - 5
D. -2 dan -5
Jawaban : B
Pembahasan
Koefisien adalah angka didepan variabel. Sehingga, koefisien dari x² – 2x – 5 adalah -2.
17. Bentuk -6x² – x + 4y variabel-variabelnya adalah ....
A. -6, -1 dan 4
B. x² , x dan y
C. x + y
D. x² – 4y
Jawaban : B
Pembahasan
Variabel adalah huruf yang ada pada suatu persamaan. Sehingga, variabel dari -6x² – x + 4y adalah x² , x dan y.
18. Hasil perkalian dari (4x - 5)(3x + 3) adalah ....
A. 12x² -3x - 15
B. 12x² +3x - 15
C. 12x² -27x - 15
D. 12x² + 27x + 15
Jawaban : A
Pembahasan
(4x - 5)(3x + 3) = 12x² + 12x – 15x – 15
= 12x² – 3x – 15
19. Hasil penjumlahan dari -3a –6b + 7 dan 13a – (-2b) + 4 adalah ....
A. 16a -8b + 11
B. 10a + 4b + 11
C. 10a -4b + 11
D. -16a -4b + 11
Jawaban : C
Pembahasan
(-3a –6b + 7) + (13a – (-2b) + 4) = (- 3a + 13a) + (-6b + 2b) + (7 + 4)
= 10a - 4b + 11
20. Diketahui bentuk aljabar 3a² -7a -9, suku yang merupakan konstanta saja adalah ....
A. 3a²
B. a
C. -7
D. -9
Jawaban : D
Pembahasan
Konstanta adalah bilangan yang tidak dimuati variabel. Sehingga konstanta dari bentuk 3a² -7a -9 adalah -9.
Bagaimana? Apakah adik adik sudah mengerti? Dengan sering berlatih soal soal matematika untuk kelas 7 SMP tersebut, maka akan membuat kamu lebih bisa untuk menguasai materi. Oleh karena itu, sebisa mungkin agar kamu terus berlatih sendiri di rumah ya. Soal yang dilengkapi dengan kunci jawaban dan juga pembahasan, akan berfungsi untuk membantu adik adik sekalian dalam memahami dan menyelesaikan soal yang sulit. Selamat mencoba!